Spørgsmål:
Hvornår er det sandt, at flere noder er lig med højere energi?
Silvio Levy
2014-07-24 08:30:11 UTC
view on stackexchange narkive permalink

Overvej alle MO'erne i et eller andet isoleret molekyle. (Det kan også være et enkelt sted; jeg bruger også MO til at henvise til AO'er.) Nummer dem i stigende rækkefølge af antallet af noder (node ​​= overflade, hvor bølgefunktionen har nul densitet). Orbitaler med det samme antal noder kan nummereres i en hvilken som helst rækkefølge. Nu har du en række orbitaler $ O_1, O_2, ... $. Lad deres respektive energier være $ E_1, E_2, ... $.

Det ser ud til at være "almindeligt kendt", at $ E_n \ le E_ {n + 1} $ for ethvert sådant system og ethvert $ n $ . Som Martin sagde det til mig i går, " En orbital med 47 noder kan aldrig have lavere energi end en med kun 46." (Opfølgning på Tælling af noderplaner i cyclopropan.)

Af forskellige årsager, der er angivet nedenfor, tror jeg, at dette ikke kan være sandt ingeneral, og jeg vil virkelig gerne vide, under hvad betingelser er det kendt at være sandt. "Kendt" her kan betyde enten en streng sætning med en henvisning til et bevis (et trivielt eksempel ville være: Det er virkelig et atom med et elektron; vi kan beregne energierne nøjagtigt) eller en præcis sætning med empirisk retfærdiggørelse (noget som "nøgneeksempler er kendt for klasse X af molekyler "- igen med henvisning).

Vigtigt : Jeg leder ikke efter en forklaring, der gentegner reglen i nogle ækvivalente eller endda løsere mode ("flere noder betyder, at orbitalen er større og mindre tæt, derfor skal den være højere inenergi").

Hvorfor tror jeg, at udsagnet ikke altid kan være sandt? Nå, et calciumatom har en fyldt 4s orbital og tomme 3d orbitaler. Hvis dette ikke tæller som et modeksempel, skal du forklare, hvad begrebet orbitalenergi udsagnet gælder for.

Generelt er jeg glad for at tro, at to MO'er skal opfylde reglen, hvis de har "sammenlignelige" sæt noder (f.eks. konstant $ n_x $ og $ n_y $ i det eksempel, jeg er ved at diskutere), men jeg vil gerne forstå, hvad der generelt forstås ved "sammenlignelig". Er der et molekyle uden symmetri overhovedet sammenlignelige MO'er? Hvis ja, hvordan ved vi, om to givne MO'er er sammenlignelige?

Tilfældet med et meget enklere system, den 3D rektangulære boks, kan også være relevant. Energiniveauerne for en sådan kasse er selvfølgelig $$ \ frac {\ hbar ^ 2 \ pi ^ 2} {2m} \ biggl (\ frac {n_x ^ 2} {L_x ^ 2} + \ frac {n_y ^ 2} {L_y ^ 2} + \ frac {n_z ^ 2} {L_z ^ 2} \ biggr), $$ hvor $ n_x $, $ n_y $ og $ n_z $ er en mere (eller en mindre, hvis du tæller væggene) end antallet af knudepunkter i den respekterede retning. Hvis vi tager $ L_x = L_y = 1 $ og $ L_z = 0.1 $ (siger), har bølgefunktionen med $ n_x = 5 $, $ n_y = 1 $, $ n_z = 1 $ energi $ 5 ^ 2 + 1 ^ 2 + ( 1 / 0.1) ^ 2 = 126 $ og 4 noder (eller 10, hvis du tæller væggene), mens bølgefunktionen for $ n_x = 1 $, $ n_y = 1 $, $ n_z = 2 $ har energi $ 402 $ og 1node ( eller 7). Så klart er reglen ikke sand her.

Indrømmet at molekyler ikke er kasser, men dette viser, at argumenter, der er baseret på antallet af tegnændringer, ikke er strenge, så de svarer ikke på mit spørgsmål. / p>

Martin - meget generøs af dig til at tilbyde en skønhed. Jeg er også forvirret over, at ingen hidtil har svaret eller fremsat kommentarer!
Jeg vil virkelig have et kanonisk svar selv. Jeg tror dog, du har ret, og min tidligere antagelse var for snæversynet. Men jeg vil virkelig gerne have lidt mere bevis. Og jeg ved, at der er mennesker i dette samfund, der kunne give mere indsigt.
Partikel i en 3D-boks følger denne regel, hvor energi skaleres med noder. Det gør også partikler i en 1D-kasse. Men det er fordi de bølger, du sammenligner, er sammenlignelige. Med 3D-rektanglet med forskellige værdier på L (for x, y og z) kan du kun sammenligne x-, y- og z- komponenterne med * hinanden *. Du kan ikke opsummere alle noderne og foretage denne sammenligning. Ligesom du kan sammenligne 1s, 2s, 3, s osv. Med hinanden, p-orbitaler med hinanden osv., Men ikke p- og d- orbitaler. Korrelationen bryder sammen, når du gør det.
@LordStryker - tak. Svar: "Partikel i en 3D-boks følger denne regel" - Med "DENNE regel" mener du ikke den regel, jeg skrev, men din regel: "du kan kun sammenligne x-, y- og z-komponenterne med hver Andet." Fair nok. Men hvis du sætter et søm ind i kassen og ødelægger symmetrien i dette legetøjseksempel, har du ikke længere x-, y- og z-modes. Så i denne situation, HVILKEN regel følges? Med hensyn til "Du kan ikke opsummere over alle knudepunkterne og foretage denne sammenligning." - Igen: Kan du angive, hvad der gør to noder sammenlignelige, dvs. hvordan man kan fortælle, at to noder er sammenlignelige?
@SilvioLevy Du kommer med et godt punkt. Jeg har aldrig arbejdet med PIAB-eksempler i noget andet end de enkle 1D / 2D-eksempler, terninger og rektangler. Partikel i et 'funhouse'? Jeg ville elske at se nogen udarbejde et sådant eksempel.
Selvom vi stadig ikke har modtaget et godt svar her, forbedrede vi i det mindste opmærksomheden om hele problemet, hvilket jeg synes er en god ting. Dette kan være et spørgsmål, der vil genere mig igen og igen. Ligesom $ \ alpha $ -effekten. http://chemistry.stackexchange.com/q/7460/4945
@SilvioLevy Et modeksempel til antagelsen om, at flere noder fører til højere energi, kan findes i homonukleære diatomiske molekyler af grundstoffer, der er tungere end $ \ ce {N} $. I dem har du meget lidt s, p-blanding og / eller relativt lidt p, p - $ \ pi $ -overlap. I sådanne tilfælde får du kvalitativt MO-ordningen vist [her] (http://www.forgottenplanet.com/studyguide/chem210/ch3_3-28.jpg). Der kan du se, at $ \ sigma $ orbital dannet af 2 p-orbitaler har lavere energi end $ \ pi $ orbitaler dannet af 2 p-orbitaler. Alligevel har $ \ sigma $ orbital 2 noder, mens $ \ pi $ orbital kun har 1.
Når jeg tænker på mit modeksempel igen, er jeg ikke længere så sikker på, at det faktisk er et modeksempel. Fordi nodeplanerne på de 2 p-orbitaler ikke forbliver parallelle i $ \ sigma $ -MO. Det er sandsynligt, at de bøjer mod hinanden. Jeg er ikke sikker på, om de rent faktisk vil smelte ind over hinanden over og under båndet midt og danne en slags ovalt formet knudeplan, eller om de kun vil bøje sig mod hinanden på et asymptotisk måde ved uendeligt (denne anden mulighed synes for at være mere tilbøjelige til mig). Ikke desto mindre er eksemplet ikke så tydeligt som jeg troede.
Ja, 3 $ \ sigma_g $ <1 $ \ pi_u $ giver et modeksempel, tak. Den alternative hypotese ville betyde, at den blå lap er rumligt afgrænset, dvs. der er en sfære uden for hvilken bølgefunktionen har det samme tegn overalt. Men dette er kun muligt, hvis det er sfærisk symmetrisk. Jeg prøver at komme med en reference eller et bevis.
Jeg sætter pris på, at dette måske ikke var det svar, vi ledte efter. Jeg tildelte dusøren alligevel, da det i det mindste giver mere information om emnet. Vi bliver muligvis nødt til at se det hele igen om et stykke tid: D
Mange tak! Jeg er nybegynder og var ikke sikker på, hvem der skulle tildele beløbet, men jeg er enig i, at Philipps svar helt sikkert fortjener det.
En svar:
Philipp
2014-08-02 22:59:54 UTC
view on stackexchange narkive permalink

Generelt tilfælde

Der er faktisk en matematisk sætning, der beskæftiger sig med antallet af noder, en egenfunktion svarende til en bestemt egenværdi kan have. Det blev fastlagt af Courant $ ^ {[1, 2]} $ og det angiver følgende:

Givet den selvtilhængende anden ordens (delvise) differentialligning

\ begin {ligning} \ venstre (\ hat {L} + \ lambda \ rho (\ mathbf {x}) \ right) u (\ mathbf {x}) = 0 \ end {ligning}

(hvor $ \ hat {L} = L (\ mathbf { \ Delta}, \ mathbf {x}) $ er en lineær, hermitisk differentiel operator, $ \ rho (\ mathbf {x}) $ er positiv og afgrænset, og $ \ lambda $ er egenværdien) for et domæne $ G $ med homogene randbetingelser, det vil sige $ u (\ mathbf {x}) = 0 $ på grænsen for regionen $ G $; hvis dens egenfunktioner er ordnet efter stigende egenværdier, så noder på $ n ^ {\ text {th}} $ egenfunktion opdeler domænet i ikke mere end $ n $ underdomæner. Nodsættet med $ u (\ mathbf {x}) $ defineres som sæt af punkter $ \ mathbf {x} $, således at $ u (\ mathbf {x}) = 0 $. Der antages ikke antagelser om antallet af uafhængige variabler.

Beviset er snarere involveret, og så vil jeg ikke vise det her. Men hvis du vil, kan du slå det op i [1] eller her.

Så Courants nodelinjesætning fortæller os, at hvis vi bestiller tidens mulige energiværdier -afhængig Schroedinger-ligning som $ \ lambda_1 \ leq \ lambda_2 \ leq \ lambda_3 \ leq \ dots $, derefter (afhængigt af præcis hvordan du indstiller nummereringen) $ n ^ {\ text {th}} $ egenfunktion, $ \ Psi_ {n} $ (den med energi-egenværdi $ \ lambda_n $) har højst $ n $ noder (inklusive den trivielle ved grænsen $ \ mathbf {x} \ til \ infty $) . Desværre giver dette dig kun en øvre grænse for antallet af noder, som en bølgefunktion med en bestemt energi-egenværdi måtte have. Så alt hvad vi ved er, at grundtilstandsbølgefunktionen $ \ Psi_ {1} $ ikke kan have nogen noder inden for regionen $ G $ (i alt har den en node, nemlig den ved $ \ mathbf {x} \ to \ infty $). Bølgefunktioner for højere $ n $ kan have op til $ n-1 $ noder inden for $ G $, men kan lige så godt have mindre. Således kan vi generelt ikke sige, at hvis en bølgefunktion har flere noder end en anden, svarer den automatisk til en tilstand med højere energi.

Specielt tilfælde: Schroedinger-ligning i en dimension

Der er dog et specielt tilfælde: For Sturm-Liouville egenværdiproblemet (og dermed for almindelige andenordens differentialligninger med homogene randbetingelser) kan vi styrke Courants teori om knudelinje sådan at hvis vi bestiller de mulige egenværdier som $ \ lambda_1 \ leq \ lambda_2 \ leq \ lambda_3 \ leq \ dots $, så er $ n ^ {\ text {th}} $ egenfunktion (den med energi egenværdi $ \ lambda_n $ ) har nøjagtigt $ n $ noder (inklusive den trivielle ved grænsen $ \ mathbf {x} \ til \ infty $).

Dette er nyttigt, da den endimensionelle tidsuafhængige Schrödinger ligning er et specielt tilfælde af en Sturm-Liouville ligning. Så i tilfælde af den inhomogene radiale Schrödinger-ligning med et lokalt potentiale og knudeløs inhomogenitet, såsom den radiale Schrödinger-ligning for det hydrogenatom

\ begin {ligning} \ bigg (\ frac {- \ hbar ^ {2}} {2 m _ {\ mathrm {e}}} \ frac {\ mathrm {d} ^ {2}} {\ mathrm {d} r ^ {2}} + \ frac {\ hbar ^ { 2}} {2 m _ {\ mathrm {e}}} \ frac {\ ell (\ ell + 1)} {r ^ {2}} - \ frac {Z e ^ {2}} {2 m _ {\ mathrm {e}} r} - E \ bigg) r R (r) = 0 \ end {ligning}

det er generelt rigtigt, at en bølgefunktion med flere (radiale) noder altid skal svare til en tilstand med højere energi end en bølgefunktion med mindre radiale noder. Det er også klart, at bølgefunktionerne i den endimensionelle partikel-i-en-boks skal følge denne regel. Men for den tredimensionelle partikel-i-en-boks er dette ikke længere sandt, da i så fald Schroedinger-ligningen i systemet ikke er en almindelig andenordens differentialligning, men en delvis-differentialligning, for hvilken kun den generelle version er af Courants knudepunkt sætning holder.

Nogle afsluttende bemærkninger

For virkelige systemer som molekyler eller krystaller er Schroedinger ligningen en delvis differentialligning, som det specielle tilfælde, der er skitseret ovenfor, ikke gør for ' t gælder, så kun Courants noderelinjesætning i dens generelle form holder, hvilket ikke giver en streng begrundelse for udsagnet om, at flere noder betyder højere energi. Alligevel observeres det meget ofte, at antallet af noder faktisk stiger med stigende energi. Årsagen til dette kan motiveres på følgende måde: Den kinetiske energi $ E _ {\ mathrm {kin}} $ for en tilstand er proportional med $ \ int \ Psi \ Delta \ Psi \, d ^ {3} r $. Via Gauss's sætning kan det vises, at $ \ int \ Psi \ Delta \ Psi \, d ^ {3} r \ propto \ int | \ nabla \ Psi | ^ {2} \, d ^ {3} r $ og så $ E _ {\ mathrm {kin}} \ propto \ int | \ nabla \ Psi | ^ {2} d ^ {3} r $. Nu tvinger noder en bølgefunktion til at ændre dets tegn. Dette betyder ofte, at værdien af ​​$ \ Psi $ skal stige / falde temmelig hurtigt, hvilket fører til områder med høje absolutte værdier for gradienten og dermed til høj kinetisk energi. Da de potentielle energier ikke bør afvige for meget mellem de forskellige tilstande, medfører den højere kinetiske energi normalt også en højere total energi. Som et eksempel kan du overveje båndfunktionerne til binding og antikondensering af et homonukleært diatomisk molekyle, hvis atomer er placeret i positionerne $ r _ {\ mathrm {A}} $ og $ r _ {\ mathrm {B}} $.

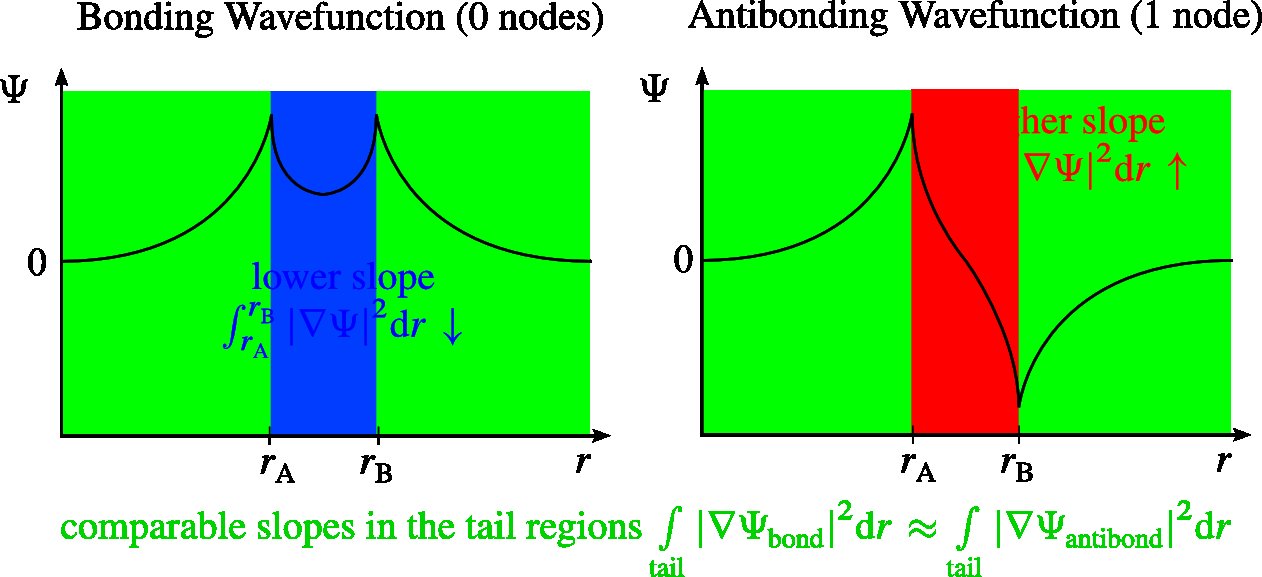
enter image description here

Bindingens bølgefunktion har ingen noder. Dens værdi mellem atomerne behøver ikke at gennemgå en hurtig ændring, og hældningen er derfor ret lav. Den antikondenserende bølgefunktion har en knude mellem atomerne. Dens værdi mellem atomerne skal ændre sig hurtigt fra dens positive til dens negative maksimum og dermed medføre en meget høj hældning. Haleregionernes skråninger er sammenlignelige for båndfunktionerne og antikondensering af bølger, da det glat kan falde til nul ved uendeligt og ikke kræves at gå fra en maksimumsværdi til nul inden for et meget begrænset område af rummet - således selvom en bølgefunktion har for at starte med en højere maksimal værdi vil gradienten ikke være meget højere. Det følger heraf, at den anti-bindende bølgefunktion har en højere kinetisk energi end bindingsbølgefunktionen.

Referencer

[1] R. Courant, D. Hilbert, Methods of Mathematical Physics , bind. 1, Interscience, New York, 1953 , s. 451-455.

[2] R. Courant, "Ein allgemeiner Satz zur Theorie der Eigenfunktionen Selbstadjungierter Differentialausdrücke", Nachr. v. d. Ges. d. Wiss. zu Göttingen 1923 , s. 81.

Tak for svaret, Philipp. Courants sætning er smuk, men den er langt svagere end den generelle påstand, da normalt i dimension d> 1 synes antallet af egenbølger med n noder at vokse nogenlunde med $ n ^ d $. Jeg håbede, at der kunne være nogle strenge resultater, der har praktisk brug. Dine afsluttende bemærkninger er ganske interessante, men igen synes den intuitive begrundelse kun at være streng i 1D. Også din første kommentar til spørgsmålet giver et modeksempel, når symmetrierne er forskellige, selv for homonukleære 2-atomsystemer.
Et andet spørgsmål til @Philipp: IIRC hypoteserne i Courants sætning er opfyldt af den tidsuafhængige, ikke-relativistiske Schrödinger-ligning, men ikke af relativistiske versioner som Klein-Gordon-ligningen. Er dette rigtigt, eller er jeg forvirret?
@SilvioLevy Jeg er bange for, at du ikke kan gøre det bedre end Courants sætning. Det antyder stærkt, at det simpelthen ikke generelt er sandt, at flere noder betyder højere energi. Men forbindelsen mellem kinetisk energi og gradient af bølgefunktionen giver en vis begrundelse for, hvorfor det er sandt det meste af tiden. Hvor meget mere praktisk brug vil du have?
@SilvioLevy Også, hvorfor tror du, at min intuitive begrundelse kun er streng i 1D? Det involverer gradienten, ikke det første afledte. Jeg valgte kun et 1D-eksempel, fordi det var lettere at visualisere.
"Hvor meget mere praktisk brug vil du have?" Noget, der giver dig mulighed for at forudsige i et tilfælde af interesse eller endda en slags statistisk måling - du siger "det meste af tiden", men jeg kan ikke se, hvordan dit argument om, at "flere noder betyder højere kinetisk energi" retfærdiggør at (hvis det virkelig var sandt, ville det være sandt hele tiden; hvis det er sandt under visse betingelser, leder jeg efter forholdene; bortset fra det forstår jeg ikke, hvad det betyder for det at være sandt "det meste af tid").
"hvorfor tror du, at min intuitive begrundelse kun er streng i 1D" - fordi konsekvensen af ​​retfærdiggørelsen mislykkes i d> 1, det er hele pointen med mit spørgsmål.
@SilvioLevy Ah, kan jeg se. Jeg er ikke matematiker af erhverv (slet ikke), så jeg er bestemt ikke opdateret med udviklingen omkring dette emne. Måske er der nogle stærkere sætninger for "praktiske" Schroedinger-ligninger, men jeg har ikke hørt om dem. Hvad angår "konsekvensen af ​​retfærdiggørelsen mislykkes i d> 1": proportionaliteten mellem kinetisk energi og $ | \ nabla \ Psi | ^ {2} $ skal være sund. Men selvfølgelig kan potentiel energi i nogle tilfælde spille en større rolle, så konsekvensen for den samlede energi er lidt håndbølgende - det er sandt.
For at være klar er problemet $ E _ {\ mathrm {kin}} \ propto | \ nabla \ Psi | ^ {2} $, som skal have en integral på højre side. Du kunne kun have høje $ | \ nabla \ Psi | $ i et lille område og stadig få en lavere samlet energi end på en anden bølgefunktion med lidt lavere $ | \ nabla \ Psi | $ over et større område.
@SilvioLevy Åh, ja. Undskyld, jeg var sjusket der. Selvfølgelig skal der være integraler. Jeg vil ændre dette i mit svar.
Det er noget, jeg også tænker på ved lejlighed. Måske kan man køre intuitionen lidt længere. Overvej $ d = 3 $ i centrale symmetriske felter. Her hjælper symmetri med at gætte, at man i sådanne tilfælde kan opdele bølgefunktionerne i familier (naturligvis svarende til irreps). Derefter tænker man på, om forholdet holder * inden for * hver familie. En anden måde at se det på er, at vi har tre frihedsgrader til at distribuere knudeplaner, der på en eller anden måde finder en passende symmetri-tilpasning.
Men det er sandsynligt, at der mellem forskellige familier vil være forvirring af energibestillingen v.s. antal noder. En anden uddannende legetøjsmodel i den forstand kan være en partikel i en 3D-kasse med forskellige kantlængder $ a, b, c $. I den sammenhæng ville det være meget sjovt at se, om der er dybere funktionelle relationer inden for en familie, som en stige op / ned generator, det være sig kun nogle omtrentlige ....


ⓘ
Denne spørgsmål og svar blev automatisk oversat fra det engelske sprog.Det originale indhold er tilgængeligt på stackexchange, som vi takker for den cc by-sa 3.0-licens, den distribueres under.
Loading...