tl; dr : Der er sandsynligvis ikke en Fe – Fe-binding. Vi bør sandsynligvis stoppe med at tegne et Fe-Fe-bånd. Lærebøger og undervisere bør virkelig stoppe med at undervise studerende om, at der er et Fe-Fe-bånd. Men alt det sagt er der ikke en enkelt tilfredsstillende forklaring på, hvorfor der ikke er en ...

På trods af mange undersøgelser (og på trods af $ \ ce {[Fe2 (CO) 9]} $ er et af de tidligste eksempler på et molekyle med symmetrisk brodannende carbonyler), karakteren af ​​binding i $ \ ce {[Fe2 (CO) 9]} $ er stadig lidt svært at få et klart billede af.

Mens de fleste akademikere på forskningsniveau nu accepterer, at der ikke er nogen signifikant bindingsinteraktion mellem de to metalcentre gentages dette ikke på bachelorniveau, hvor Fe-Fe-bindingsmodellen stadig undervises.

De fleste lærebøger undgår enten problemet helt (giver aldrig en struktur) eller viser Fe-Fe-binding (med en fodnote om, at det måske ikke er korrekt), og selv dem, der anerkender manglen på metal-metalbinding (Elschenbroich er et godt eksempel), diskuterer ikke rigtig, hvordan dette fungerer i praksis, eller hvordan man ville gå omkring elektron optælling (en kilde til mange et grimt selvstudieproblem).

Historisk sammenhæng

Det enkle svar er, at der aldrig rigtig var nogen stærke beviser for tilstedeværelsen af ​​Fe-Fe-båndet. Som det ofte er tilfældet, blev det adopteret af flere (velkendte) kemikere på det tidspunkt, og efterfølgende publikationer (og især lærebøger) udbredte ideen, hovedsagelig på grund af dens bekvemmelighed med hensyn til elektronoptælling.

De tidligste data, der virkelig kiggede på karakteren af ​​Fe – Fe-båndet i $ \ ce {[Fe2 (CO) 9]} $ kan tilskrives en krystalstruktur målt ved Powell (2,46 Å) ^[1] (senere korrigeret med bomuld (2,53 Å)). ^[2]

Selvom disse værdier ikke nødvendigvis beviser eksistensen af ​​en Fe – Fe-binding (du kan ikke se en binding med røntgen, kun atomer, hvorfra du kan udlede binding), var dets tilstedeværelse nødvendig for at opfylde 18-elektronreglen, og de opnåede værdier var i overensstemmelse med andre kendte M-M-bindingslængder.

Problemet med ovenstående argument (så praktisk som det er) er, at det er umuligt at fortælle, om 2.53 Å repræsenterer en sand bindingsinteraktion, eller om det simpelthen er en konsekvens af den brodannende Fe – C (O) –Fe-bindinger, der trækker metaller tæt på hinanden. Selve jernet er relativt kontraheret, så i modsætning til i nogle andre broforbundne systemer er det steriske problem med at bringe de to metaller sammen relativt minimalt.

Begyndelsen på forandring

Selvom Fe-Fe-båndet blev vedtaget temmelig vidt, var ikke alle enige.

Roald Hoffmann (af Woodward – Hoffmann-berømmelse) offentliggjorde flere artikler, der syntes at modsige tilstedeværelsen af ​​en Fe-Fe binding, hvilket viser, at interaktionen faktisk var "antikondenserende og frastødende". orbitale diagrammer ved hjælp af molekylær symmetri og isolobale / elektroniske fragmenter (fra velopførte molekyler) for at samle den sandsynlige binding i $ \ ce {[Fe2 (CO) 9]} $ . Til dato er hans fund stort set stadig gyldige (skønt nøjagtige energier nu er beregnet med langt mere nøjagtighed).

Kvantitative beregningsstudier ^[#]

Moderne beregningsundersøgelser er enige om, at Fe-Fe-interaktionen generelt er netto anti-binding (selvom der er fundet nogle bindingsinteraktioner) uden ægte kovalent Fe-Fe-binding, da blev oprindeligt foreslået.

I Liddles Molecular Metal-Metal Bonds giver McGrady et kvalitativt molekylært orbitaldiagram for komplekset. Orbitalerne σ og σ * såvel som δ _π og δ _π * orbitalerne (klemt mellem det tidligere par) er fuldt optaget og giver ingen nettobindende karakter. Imidlertid fører populationen af ​​Fe-Fe-antistofbindende π _δ * orbitaler til en formel bindingsrækkefølge på –2. ^[4]

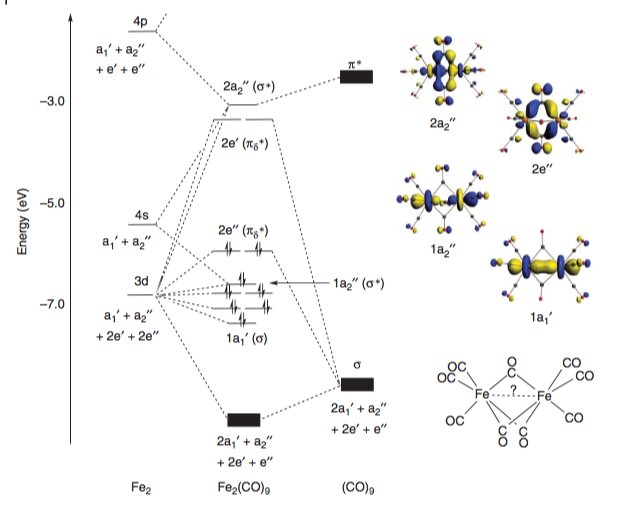Dette diagram korrelerer godt med resultaterne i en af ​​de tidligste beregningsundersøgelser på dette system, der sammenligner forskellige metoder (DFT, MP2, SCF) af Reinhold. ^[5]

I undersøgelsen beregnes forskellige egenskaber for molekylerne (M – M bindingslængde, M – C bindingslængder, bindingsvinkler osv.), og disse data sammenlignes med kendte data fra krystalstrukturer / andet eksperimentelt arbejde. De bestemmer, at kun DFT giver nøjagtige resultater (rejser tvivl om tidligere beregningsarbejde ved hjælp af mindre stringente metoder). ^[##]

Det konstruerede molekylære orbitale diagram (i overensstemmelse med en fra Ref [4] ovenfor) viser afgørende, at der observeres en negativ overlapning af Fe-Fe orbitaler, hvilket antyder en direkte frastødning. For at citere direkte fra papiret:

i jernsystemerne med mere kontraherede metalorbitaler er den direkte metal-metal-frastødning relativt svag, mens metalbro-bindingerne er tilstrækkelig stærke

Andre beregningsundersøgelser har set at beregne kompleksets egenskaber, såsom vibrationsfrekvenser af enhver foreslået Fe-Fe-binding eller NMR-afskærmninger, der ville være til stede på liganderne med og uden tilstedeværelsen af ​​Fe –Fe bond. Dette arbejde henvises til i Comprehensive Organometallic Synthesis II (bind 6), men synes ikke at have ført til meget nyttige resultater.

Konklusion

Medtagelsesmeddelelsen fra dette er, at der virkelig ikke er sandsynlighed for, at der er en Fe-Fe-bånd på den måde, som det ofte læres at studerende, og bestemt ikke med henblik på elektrontælling.

A god mulig forklaring gives af McGrady, ^[4] , som giver en forklaring på, hvorfor 18-elektronreglen ikke er vigtig i dette tilfælde (og på et niveau, som en studerende kunne forstå):

Der er faktisk mange paralleller mellem 34-elektron $ \ ce {[Fe2 (CO) 9]} $ og kvadrat- plan 16-elektronarter, ikke mindst begge tendensers reaktion med nukleofiler. Opdelingen af ​​18-elektronreglen i kvadrat-plane komplekser opstår, fordi den ledige p _z orbital ikke finder en passende symmetri match blandt de lineære kombinationer af ligandbaserede orbitaler og anvendes således ikke, hverken til at danne en binding eller til at rumme metalbaserede ensomme elektronpar. [...]

I $ \ ce {[Fe2 (CO) 9]} $ er der to ledige $ \ mathrm {a_2 ''} $ -symmetriske metalbaserede kombinationer (primært lineære kombinationer af 4'er og 4p _z ) men kun en optaget ligandbaseret kombination af den samme symmetri. Således forbliver en af ​​de to metalbaserede orbitaler "ubrugte" i samme forstand som p _z orbitalen forbliver ubrugt i kvadrat-plane arter. Denne enkle symmetri-baserede analyse antyder, at der ikke er behov for at påberåbe sig en Fe-Fe-binding i $ \ ce {[Fe2 (CO) 9]} $ simpelthen fordi metalcentre overholder ikke 18-elektronreglen.

Referencer & Notes

^{[1] : Powell, HM; Ewens, R.V.G J. Chem. Soc 1939 , 286}

^{[2]: Cotton, F.A .; Troup, J.M. J. Chem. Soc. Dalton Trans. 1974 , 800}

^{[3]: Lauher, J.W .; Elian, M .; Summerville, R.H .; Hoffman, R. J. Er. Chem. Soc. , 1976 , 98 , 3219}

^{[#]: Fuld offentliggørelse, jeg har læse de fleste papirer, der følger på et tidspunkt, mens du prøver at besvare dette tidligere, men (stor men) Jeg er ikke en beregningskemiker. Jeg håber, at en anden muligvis kan kaste lys over, hvor gyldige disse beregningsresultater faktisk er.}

^{[4]: ​​McGrady, J.E. i Molecular Metal – Metal Bonds ; Liddle, S., red .; Wiley-VCH: Weinheim, 2015}

^{[5]: Hunstock, E .; Mealli, C .; Jose-Calhorda, M .; Reinhold, J. Inorg. Chem. 1999 , 38 , 5053. Bemærk, at dette ikke er en komplet geometrioptimering, de starter med nogle kendte parametre . New J. Chem. 1994 , 18 , 465 er et papir, der angiveligt forsøger fuldstændig optimering fra bunden, men jeg kan ikke finde det nogen steder lige nu for at få adgang til det}

^{[##]: Selv nu er der mange problemer med nøjagtigt beregning af organometalliske kompleksers egenskaber ... det tager en enorm enorm mængde beregningstid på grund af behovet for basissæt langt udvidet sammenlignet med dem, der er udviklet til enkle organiske systemer}

For at supplere det accepterede svar er her noget andet, jeg fandt.

Limning ved brodannelse af carbonyler

En alternativ forklaring på limningen i $ \ ce {[Fe2 (CO) 9]} $ er præsenteret i en artikel fra Green ¹ fra 2012 (som også indeholder adskillige henvisninger til tidligere beregningsstudier, der indikerer fravær af en obligation ). I det beskriver forfatterne Fe – C (O) –Fe-bindinger som to ”typer”. Hvis der er tilbagebinding fra metal til carbonyl π *, er den brodannende carbonyl "ketonisk" i naturen; hvis der ikke er nogen backbonding, kan interaktionen bedst beskrives som 3-center-2-elektron (3c2e).

(The halvpil her er ikke relateret til nogen form for radikale reaktioner - det er for at "understrege, at donoratomet ikke bruger to ensomme par, men snarere at et enkelt elektronpar deles med begge atomer", i forfatternes ord .)

Hvilken af ​​disse to ordninger, der er passende, afhænger i alt væsentligt af besættelsen af ​​orbitale (r), der er mærket $ \ lambda- $. Denne orbital er dannet af Fe 3d og CO π * orbitaler, og man kan se, at den svarer til $ \ mathrm {2e ''} $ orbitaler i MO-diagrammet leveret af NotEvans.

Artiklen derefter fortsætter med at tilvejebringe et kvalitativt MO-diagram for komplekset ved hjælp af Hoffmanns tidligere tilgang ² , som påberåber sig den isolobale analogi.

Det, der skal bemærkes her, er at der er tre brodannende carbonylligander, men der er kun to backbonding, $ \ lambda- $ type orbitaler at udfylde (af symmetri $ \ mathrm {e ' '} $). Derfor er to af de tre brodannende carbonyler "ketoniske"; den tredje brodannende carbonyl kan bedst beskrives som involveret i en Fe-C (O) –Fe 3c2e-binding.

Er der en binding ?

Ifølge til forfatterne kan $ \ mathrm {a_1 '} $ orbital, der er dannet af jern $ \ mathrm {d} _ {z ^ 2} $ orbitaler, ikke tælle som en Fe-Fe σ binding, fordi disse d orbitaler er stærkt involveret i backbonding til terminale carbonyler.

$ \ mathrm {e '} $ MOs (som svarer til $ \ lambda + $ orbitaler i det første diagram og har Fe – Fe π-binding i karakter) og $ \ mathrm {e' '} $ MOs ( $ \ lambda- $ orbitaler, Fe – Fe π-antibonding) er begge optaget og kan ikke føre til nogen nettobinding. Faktisk er bindingen $ \ mathrm {e '} $ orbitaler for det meste centreret om CO, mens de anti-bindende $ \ mathrm {e' '} $ orbitaler for det meste er centreret om Fe. Så der er en netto frastødende interaktion mellem de to jernatomer i overensstemmelse med beregningsstudier.

Forhold til 18-elektronreglen

Når vi går tilbage til de to typer brodannende carbonylligander, tæller den første "ketoniske" carbonylligand som en en-elektron-donor til begge metalatomer, som det normalt læres i indledende organometallisk kemi. I elektrontællingsnotation skrives dette normalt som μ-X ₂ , hvilket indikerer, at carbonylliganden er en en-elektron-donor (X) til de to metalatomer, den overbygger.

3c2e-liganden tæller dog som en to-elektron donor til begge metalatomer. Det er ikke, at liganden donerer to elektroner til hvert metalatom (hvilket er umuligt her, da CO kun kan donere et enkelt par på kulstof). I stedet donerer liganden to elektroner til hele broen, som deles mellem begge metalatomer. Dette kan betegnes μ-L ₂ (L angiver en to-elektron donor).

Ved hjælp af denne formalisme er det let at se, at 18-elektronreglen er opfyldt for begge jerncentre, hvis vi antager, at de tre brodannende carbonyler består af to μ-X ₂ carbonyler og en μ-L ₂ carbonyl:

Da de tre brodannende carbonyler er ækvivalente, kan vi naturligvis ikke udpege nogen af ​​dem til at være μ-L ₂ carbonyl ; det er teknisk mere nøjagtigt at betragte det som en hybrid af tre resonansstrukturer, der hver har en anden brodannende carbonyl, der er μ-L ₂ .

Referencer

1. Green, J. C .; Green, M. L. H .; Parkin, G. Forekomsten og repræsentationen af ​​tre-center to-elektronbindinger i kovalente uorganiske forbindelser. Chem. Commun. 2012, 48 (94), 11481–11503. DOI: 10.1039 / C2CC35304K.

2. Summerville, R. H .; Hoffmann, R. M ₂ L ₉ komplekser. J. Er. Chem. Soc. 1979, 101 (14), 3821–3831. DOI: 10.1021 / ja00508a019.